3+1 Dissipative Space out of
Quantum Mechanics
by
Michael Manthey Douglas Matzke
April 2012.
Abstract. We report the discovery of two dual and emergent sets of three irreversible bi-vectors – dubbed the TauQuernions – that are otherwise isomorphic to quaternions. This inherently dissipative 3-dimensional tauquernion space is a subspace of the geometric (Clifford) algebra
with generators
; a straightforward mapping then produces a 3+1 dimensional space with signature
in
. The individual tauquernions are entanglement operators corresponding to the quantum mechanical Bell and Magic operators. The form
has 64 sign variants of which 16 are nilpotent, which latter we identify with the Higgs boson; the other 48 variants square to the unitary 4-vector
, which we identify as the carrier of mass. A natural candidate for dark matter also emerges, which we analyze. We calculate the information content of these and related forms, draw an exact map of the entropic pathways an expansion will follow, and sketch how this Bit Bang develops. Photons are clearly represented and transparently intertwined in the space, so one can expect overall compatibility with relativity theory.
Synchronization: The Font of Physical Structure
Michael Manthey
Abstract. The computational operation called synchronization, vital for realizing multi-process systems, is described in terms of geometric (Clifford) algebras over {-1,0,1}. This provides a two-way bridge between the worlds of computation and quantum mechanics, and casts new light on such matters as quantum non-determinism, mechanism and causality, the explicit structure of particles (including dark matter), and the like. We dub this the synchronizational model of quantum mechanics. Oppositely, we show how to represent any computation – sequential or concurrent – in these algebraic terms, thus providing a novel and powerful physically-oriented mathematics for computer science and allied disciplines.
Riemann Fever
Michael Manthey
December 2009.
Abstract. The confluence of computer science and quantum mechanics has inspired a proof of the Riemann Hypothesis for the discrete geometric (Clifford) algebras over
, as expected from the Weil Conjectures. The symptoms of Riemann Fever are clearly evident here – long periods of apathy punctuated by febrile investigations lasting from minutes to (here, two) weeks, accompanied by alternating explosions of euphoric insight into cosmic truths, and insight becalmed in a sea of profundity; and as well a weakness for sweeping conclusions of great import. I recount the course of the affliction in my own case of this recurrent virulent ailment, which often leads to addiction to further attacks, and other complications.
The Standard Model in 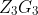
Michael Manthey
Quantum Computation using Geometric Algebra (full version)
Quantum Computation – 25p. summary
Douglas Matzke
2002
Abstract. Understanding Quantum Computing is Difficult. Classically trained computer engineers and programmers seem ill equipped to participate in the quantum computing revolution unless they have been educated in the specialized math and physics of quant um computing. The quantum computation rules are so different from classical computing that currently this field is inhabited predominantly by physicists and mathematicians. Unfortunately, many of these researchers lack the sophisticated and well developed programming skills to build the development environment tools needed to program complex and unintuitive quantum systems. This is a classic skills- mix problem and the goal is to provide the tools needed by designers of quantum computing systems.
Leave a Reply